chitanda's blog

吃蛋挞的咸鱼博客

0%

Hackenbush

发表于 更新于 阅读次数： Valine：

Hackenbush

Hackenbush 是由数学家 John Horton Conway 发明的一个双人游戏，他在组合博弈等领域颇有成果， 是组合博弈论的开创者之一，后面要讲到的 surreal number 也是他所定义和构造的。Hackenbush 有一条称之为 "ground" 的线（或者将其看作点，称之为根，这并没有什么区别）和一些端点，以及若干条线段，每条线段连接两个端点或者一个端点和 ground 线，并且每条线段都和 ground 连通。两个玩家轮流操作，每次选择一条线段删除，同时将那些和 ground 不再连通的线段也一并删除，不能操作的玩家失败。

在最初版本的 Hackenbush 中，每个玩家都可以删除任意一条线段，但在后来，又发明出了每条线段可以被配置成只能其中一个玩家删除的版本。一般来说，有三种版本：

  • Original Hackenbush: 或者称之为 Green Hackenbush，只有绿色的边，即最初版本。
  • Blue-Red Hackenbush: 蓝色的边只能由玩家一删除，红色的边只能由玩家二删除。
  • Blue-Red-Green Hackenbush: 最复杂的版本。

而每种版本，也都还有着链、树和图三种不同复杂性的区别。

接下来，我将分别介绍这三种版本，并尽量给出易懂的过程证明。

Green Hackenbush

Green Hackenbush 属于平等博弈，因此也是通过 SG 定理来解决的，让我们一步步分析。

链

这种情况也叫 bamboo stalks，由若干条链组成，这实际上就等价于尼姆博弈了，不再赘述。

树

如何计算一棵树的 \(sg\) 值是问题的关键。

Thomas S. Ferguson 的 "GAME THEORY" 中介绍了解决的方法。

Colon Principle: When branches come together at a vertex, one may replace the branches by a non-branching stalk of length equal to their nim sum.

翻译一下，就是当不同的分支在一个节点交汇时，可以用一条长为他们 \(\text{nim}\) 和的链来代替他们。实际上，这条原理对于图的情况也是适用的，不过要求不同分支之间没有其他交点。

证明：考虑一个任意一个 Hackenbush 所描述的图 \(G\) ，选择 \(G\) 中任意一个点 \(x\) ，让 \(H_1\) 和 \(H_2\) 是任意拥有相同 \(sg\) 值的图，令 \(G_1=G_x:H_1\) ，\(G_2=G_x:H_2\) ，其中 \(G_x:H_i\) 表示将 \(H_i\) 连在 \(G\) 的点 \(x\) 上（即 \(H_i\) 原本连向 ground 的边改为连向 \(x\) ）。那么，\(G_1\) 和 \(G_2\) 应该拥有同样的 \(sg\) 值 ，\(G_1+G_2\) 的 \(sg\) 值为 \(0\) ，为先手必败态：如果先手在 \(G_i\) 中原本为 \(G\) 的部分删除一条边，那么后手只需在另一个图中复制该操作，如果先手在 \(H_i\) 中操作，改变了原本 \(H_i\) 的 \(sg\) 值，那么后手也能有办法将 \(H_{3-i}\) 的 \(sg\) 值变成一样的。当 \(H_1\) 是一条长为 \(sg\) 值的链时，这意味着，\(H_2\) 能被长为其 \(sg\) 值的链所替代。

树

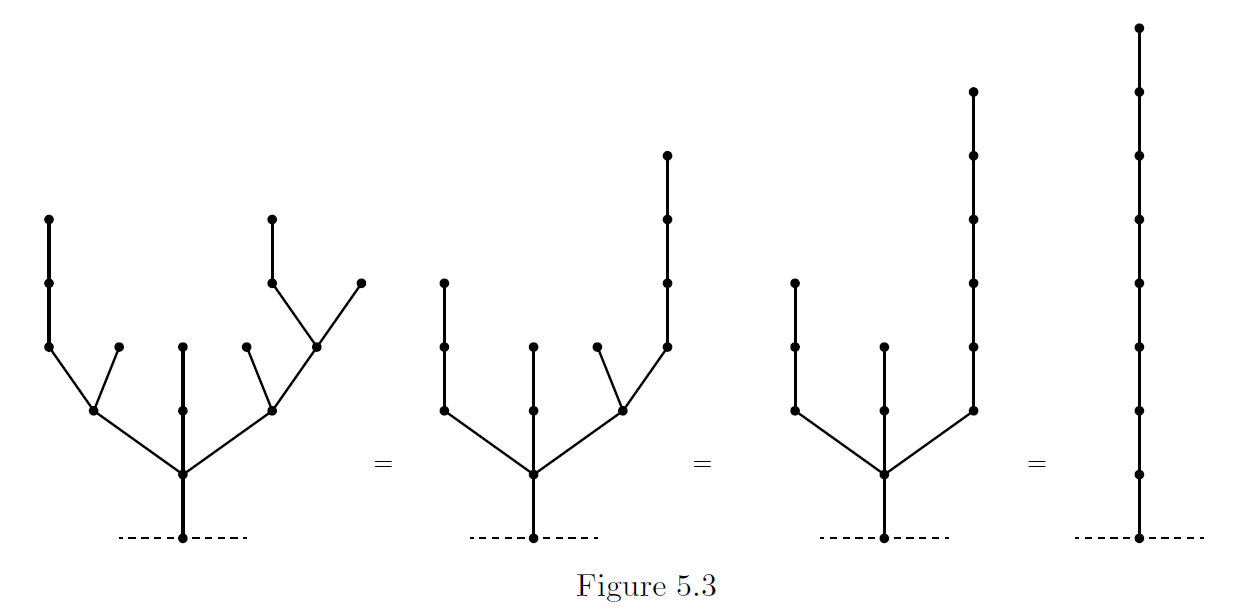
图

图的情况的复杂性在于它可以有环。

Fusion Principle: The vertices on any circuit may be fused without changing the Sprague-Grundy value of the graph.

也就是说，我们可以将环上任意两个点合并。而所有环上的点合并后，环上的一条边就变成了一条自环，而一条自环可以用一条边连着一个新点来代替。比如：

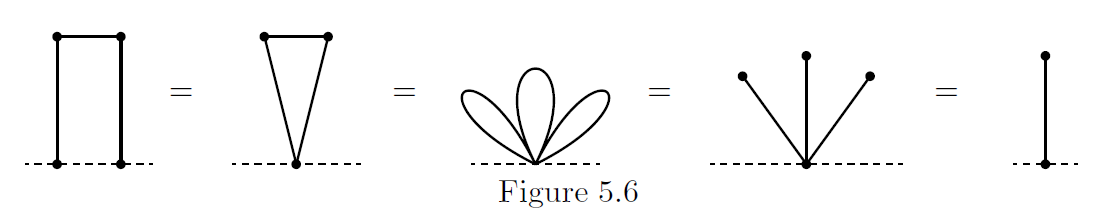
证明：我们称合并后 \(sg\) 值不变的图是好的，改变了的图是坏的。假如存在坏的图，那么选择一个边数最少（假设为 \(m\) ）并且拥有最少点数（这里，我们将 ground 当成一个点）的坏图，删除它的任意一条边都会使其变成好图，任何一次合并操作都会改变它的 \(sg\) 值。那么有以下推论：

  1. \(G\) 中不存在一对点 \(x,y\) 之间有三条或以上不相交的简单路径。否则，将合并 \(x,y\) 后的 \(G\) 称之为 \(H\) ，\(H\) 和 \(G\) 的 \(sg\) 值不同，所以 \(G+H\) 必然是先手必胜的。所以当先手删除了 \(G\) 或 \(H\) 中的一条边使得 \(sg\) 变成 \(0\) ，后手也在另一个图中删除了相应的那条边，使两个图变成拥有 \(m-1\) 条边的图 \(G'\) 和 \(H'\) ，此时 \(G'+H'\) 也是先手必胜，并且它们都是好的，然而，由于 \(x\) 和 \(y\) 之间存在三条不相交的路径，无论在 \(G\) 中如何删除，都会使得 \(x\) 和 \(y\) 仍然在一个环上，此时在 \(G'\) 中合并 \(x\) 和 \(y\) ，就会变成 \(H'\) ，这与 \(G'+H'\) 是先手必胜相矛盾。
  2. \(G\) 中的环都必须包含 ground 这个点。假设 \(G\) 中存在不包含 ground 的环 \(C\) ，那么设 \(G'\) 为 \(G\) 删除所有 \(C\) 中的边后的图（其他在删除后未与 ground 相连的部分也一并删去了），那么 \(G'\) 只剩下 \(C\) 中的一个点，如果剩下两个或以上，违背上一条推论（两个点通过 \(C\) 有两条路径相连，通过 \(G'\) 也有一条路径相连）。所以，\(C\) 以及其他一并删去的部分与 \(G'\) 之间仅通过一个点相连，通过 Colon Principle，我们可以将删去的部分（设为 \(C'\) ，显然他们是好的，可以合并）变成一条长为其 \(sg\) 值的链与 \(G'\) 相连构成一个 \(G''\)，和原本的图 \(G\) 的 \(sg\) 值相等，也就是说，\(G\) 在一系列包括合并 \(C\) 的变换后形成的 \(G''\) 与 \(G\) 的 \(sg\) 相同，这显然矛盾了。
  3. \(G\) 中只有一个环包含 ground，即，\(G\) 中只包含一个环。如果存在两个或以上，他们的交点必须只有 ground，否则与推论 1 矛盾，这种情况下，将其分成几个图，各自都是好的，这与假设矛盾。

基于以上几个推论，最小的坏的图只可能是一个包含 ground 的环，环上的点再挂一些树，而基于 Colon Principle，树都能被链替换。如果仍将 ground 看成线，那么这样的图将呈现出“桥”的形状，如下图所示，因此我们也将这个环称之为桥。接下来，我们要证明这样的 \(G\) 是好的。

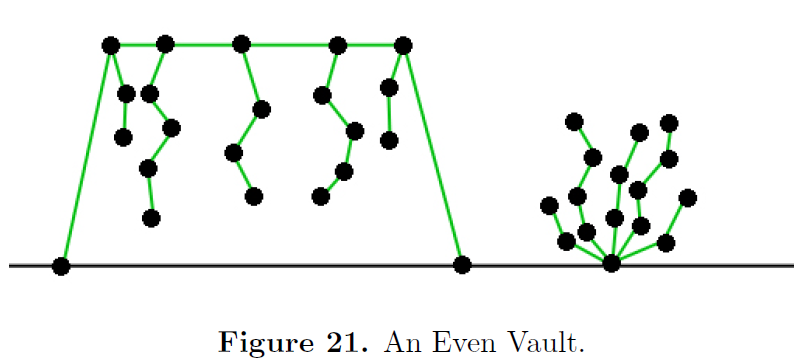
当 \(m\) 为偶数时，如图，设右边为合并了桥后的图 \(G'\) ，如果证明了 \(G+G'\) 的 \(sg\) 值为 0，就可以证明 \(G\) 是好的。如果先手删除一个图的非桥边，后手只需删除另一个图对应的边即可。如果先手删除了一条桥上的边，变成了树的情况，将使剩下的边数变为奇数，\(sg\) 值也肯定是奇数（仔细想想，这其实很显然），必然不为 \(0\) ，因此后手必胜。

当 \(m\) 为奇数时，如图，证明 \(G+G'\) 的 \(sg\) 值为 \(0\) 即可。删链上边和桥上边的情况同理，只需考虑先手删除的是单独的那条边。考虑如果 \(G\) 桥上某个点挂的链是奇数长度，设为 \(2a+1\) ，那么删除它末端的边将其变成偶数长度，由于该图边数少于 \(G\)，它是个好图，可以合并，而合并后，其他的链抵消，总的 \(sg\) 值显然为 \(2a\oplus (2a+1)\oplus 1=0\) ，其中的 \(1\) 是合并奇数长度桥所产生的。因此，只需考虑所有的链都是偶数长度的情况。

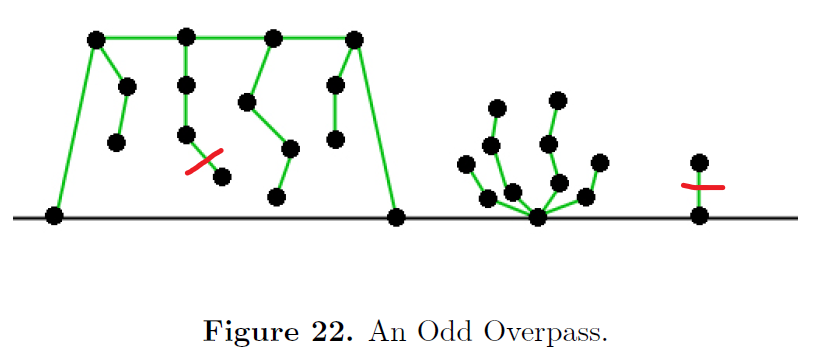
将所有桥上边黑白染色，使得桥中间的边为白色，相邻边不同色，那么白边数量为奇数，黑边数量为偶数。如果删除一条白色的边，将桥分割为两棵树，每棵树的 \(sg\) 值都是这样的形式： \[ 2a+1\oplus 2b+1\oplus 2c+1\oplus 2d+1\oplus \dots \] 这里，我们假定 \(+\) 和 \(\oplus\) 拥有同样的运算优先级，因此上面的式子是从左往右依次运算的。注意到，奇数次出现的 \(+1\) 都和 \(\oplus 1\) 等效（因为，前面运算的结果都是偶数），因此，也可以将上式写成： \[ \begin{aligned} res&=2a\oplus1\oplus 2b+1\oplus 2c\oplus 1\oplus 2d+1\oplus \dots \\ &=2a\oplus2b\oplus1+1\oplus 2c\oplus 2d\oplus 1+1\oplus \dots\\ &=2a\oplus2b+1+1\oplus 2c\oplus 2d+1+1\oplus \dots\\ &=2a\oplus2b+2\oplus 2c\oplus 2d+2\oplus \dots \end{aligned} \] 若桥上边数模 \(4\) 余 \(1\) ，删除一条白边后两棵树剩余的桥边都为偶数，那么 \(res\) 的值为偶数，而将其除二后，为 \(a\oplus b+1\oplus c\oplus d+1\oplus \dots\) 。这等价于，将原图中链长度减半并合并所有黑边，称之为减半后的图 \(\frac{G}{2}\)，再删除那条白边形成的树所计算出的 \(sg\) 值。若桥上边数模 \(4\) 余 \(3\) ，则 \(res\) 是 \(\frac{G}{2}\) 删除这条边后树的 \(sg\) 值的两倍再 \(+1\) 。

除非桥边数为 \(1\) ，这种情况显然 \(G\) 是好的，否则 \(\frac{G}{2}\) 边数必然小于 \(G\) ，它应该是好的，且桥上边数为奇数，所以，\(\frac{G}{2}+(\frac{G}{2})'\) 的 \(sg\) 为 \(0\) ，如果先手删除单独那条边，剩余的 \(sg\) 为 \(1\) ，也就是说，后手无论如何都存在删除 \(\frac{G}{2}\) 中的一条边的必胜策略。若后手的必胜策略是删桥边，在 \(G\) 中删除对应的一条白边，那么显然，形成的两棵树的 \(sg\) 值在原图和减半图中是两倍关系或者两倍加一关系，因此总的 \(sg\) 值也是两倍关系，都为 \(0\) （思考下，若 \(a\oplus b\oplus c=0\) ，那么 \((2a+1)\oplus (2b+1)\oplus 2c=(2a\oplus 1)\oplus (2b\oplus 1)\oplus 2c=0\)）。若删除的是链上的边，那么，让 \(G\) 对应的链仍保持 \(\frac{G}{2}\) 这条链的两倍，显然，这之后的图是好的，且通过合并可以知道总的 \(sg\) 值仍是两倍关系。因此，\(G+G'\) 为先手必败，其 \(sg\) 值为 \(0\) 。

综上所述，我们通过反证法证明了不存在坏的图，所有的图都是可合并的。

Blue-Red Hackenbush

Blue-Red Hackenbush 属于不平等博弈，无法继续用上面的办法来解决这个问题，但是有的思想还是可以沿用。

以下为了简便，称只能删除蓝色边的为 L，只能删除红色边的为 R。

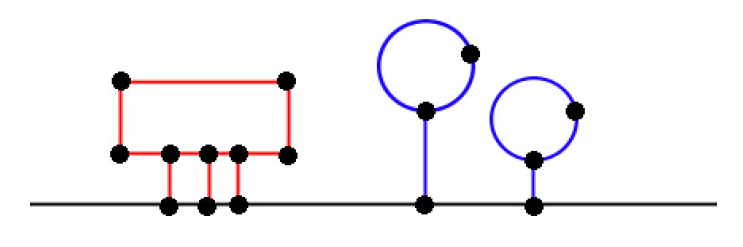
如上图，红色边有 \(10\) 条，而蓝色边只有 \(4\) 条，显然，只能删红色边的 R 必胜。

如上图，无论先手如何删边，后手都能复制其操作，因此是一个后手必胜的状态，我们称这种后手必胜的游戏为 zero games 。

显然，当红色蓝色的边都是分离的时候，通过计算蓝色边数减红色边数，即可知道胜负状态，如果是正的，那么 L 必胜，如果是负的，那么 R 必胜，如果为零，那么后手必胜。那么，是不是我们可以用一个数字来代表一个游戏的值，游戏的和的值通过加减计算，并通过值的正负来判断胜负状态呢。

当两种边不再分离，让我们看看会发生什么，先从简单的情况入手，对于下面三种情况来说，不难发现，分别是 L 必胜，R 必胜和后手必胜。

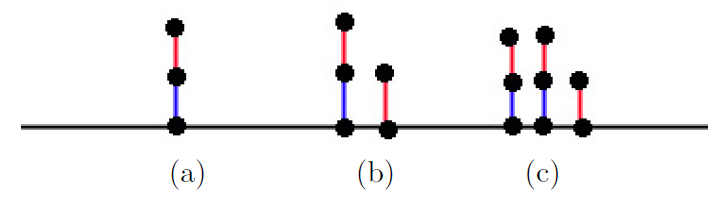
  • 对于 (a)，L 必胜，假定这个游戏的值为 \(x\) ，有 \(x\gt 0\) 。
  • 对于 (b)，R 必胜，所以有 \(x-1\lt 0\) ，那么有 \(0\lt x\lt 1\) 。
  • 对于 (c)，为 zero game，所以有 \(x+x-1=0\) ，因此可以得到 \(x=\frac{1}{2}\) 。

假设一个图 \(P\) ，由 L 操作产生的任意一个后续状态为 \(P^L\) ，由 R 操作产生的任意一个后续状态为 \(P^R\) ，\(P\) 可以通过在 \(P^L\) 上加上一条蓝边以及连接在这条蓝边上的其他边得到的，那么有 \(P>P^L\) ，即（以下不再区分图以及图的值）： \[ P^L<P<P^R\quad \text{for all}\ P^L,P^R \] （证明 \(P>P^L\) 并不难，假设有一个和 \(P^L\) 颜色相反的图 \(-P^L\) ，那么容易得到 \(P+(-P^L)\) 为 L 必胜 ）

因此，\(P\) 是介于 \(P^L\) 的最大值以及 \(P^R\) 的最小值之间的。

设 \(P\) 为：\(\{P^L_1,P^L_2,\dots|P^R_1,P^R_2,\dots\}\) ，其中 \(|\) 左边为 L 操作能到达的状态，右边为 R 操作能到达的状态，且 \(P^L\) 为所有 \(P^L_i\) 的最大值，\(P^R\) 为所有 \(P^R_i\) 的最小值，那么 \(P\) 和 \(P'=\{P^L|P^R\}\) 等价。

证明：设 \(P'\) 颜色相反的图 \(-P'=\{-P^R|-P^L\}\) ，有 \(P+(-P')\) 这个游戏，不失一般性的假设 L 先手，若它选择一个后续状态 \(P^L_i+(-P')\) ，且 \(P_i^L<P^L\) ，那么 R 将游戏操作为 \(P^L_i+(-P^L)<0\) ，R 必胜，因此 L 必不可能选择这样一个操作。而如果 L 选择 \(P^L\) ，则后手操作为 \(P^L+(-P^L)=0\) 。如果 L 选择操作 \(-P'\) 变为 \(-P^R\) ，R 只能选择后续状态为 \(P^R+(-P^R)=0\) 。因此 \(P+(-P')=0\) ，故 \(P=P'\) 。

Surreal Number

中文译作超现实数，最早由 John Horton Conway 定义和构造，并在著作《 论数字与博弈》（On Numbers and Games） 中进行了描述。这是一套全新的数学系统，你必须忘记所有你之前知道的关于“数”的概念，包括数的大小等于关系！当然，如果你有基础，可以从代数的角度去理解它。

构造

超现实数的构造方法是递归的，设 \(L\) 和 \(R\) 是两个超现实数的集合，并且不存在 \(x\ge y,x\in L,y\in R\) （这里 \(\ge\) 的定义稍后给出），那么 \(\{L|R\}\) 也是一个超现实数。例如，\(\{\varnothing|\varnothing\}\) 就是一个最简单的超现实数，它也是构造一切超现实数的起点。

约定

设一个超现实数 \(x=\{L|R\}\) ，我们用 \(x^L\) 表示 \(L\) 中的元素，\(x^R\) 来表示 \(R\) 中的元素，并且将 \(x\) 写作 \(\{x^L|x^R\}\) 。即，若 \(L=\{a,b,c,\dots\},R=\{d,e,f,\dots\}\) ，那么 \(x=\{L|R\}\) 写作 \(\{a,b,c,\dots|d,e,f,\dots\}\) 。

定义

定义 \(x\ge y,x\le y\) 。

\(x\ge y\) 当且仅当 \(\forall x^R,x^R\nleq y\) 且 \(\forall y^L, x\nleq y^L\) 。简单的说，就是不存在 \(x^R\le y\) 且不存在 \(x\le y^L\) 。

\(x\leq y\) 当且仅当 \(y\leq x\) 。即 \(x^L\ngeq y\) 且 \(x\ngeq y^R\) 。

其中 \(x\nleq y\) 即 \(x\le y\) 不成立。

可以发现，这里的定义也是递归的。

一个显而易见的结论：若不存在 \(x^R\) 且不存在 \(y^L\) ，那么 \(x\ge y\) 必然成立。

定义 \(x=y,x>y,x<y\) 。

\(x=y\) 当且仅当 \(x\ge y\) 且 \(x\le y\) 。

\(x>y\) 当且仅当 \(x\ge y\) 且 \(x\nleq y\) 。

\(x<y\) 当且仅当 \(y>x\) 。

定义 \(x+y\) 。

\(x+y=\{x^L+y,x+y^L|x^R+y,x+y^R\}\) 。

定义 \(-x\) 。

\(-x=\{-x^R|-x^L\}\) 。

定义 \(xy\) 。

\(xy=\{x^Ly+xy^L-x^Ly^L,x^Ry+xy^R-x^Ry^R|x^Ly+xy^R-x^Ly^R,x^Ry+xy^L-x^Ry^L\}\)

用有理数来表示超现实数

我们想要用一个具体的数来代表一个超现实数。首先，令 \(\{\varnothing|\varnothing\}=\{|\}=0\) 。可以发现，\(0\ge 0\) 。

那么 \(\{0|\},\{|0\},\{0|0\}\) 呢？首先注意，由于 \(0\ge 0\) ，\(\{0|0\}\) 是不符合定义的，不属于超现实数。再根据定义有 \(\{0|\}\ge 0\) 且 \(\{0|\}\nleq 0\) ，即 \(\{0|\}>0\) ，同理可得 \(\{|0\}<0<\{0|\}\) 。那么令 \(\{0|\}=1\) ，\(\{|0\}=-1\) 。

现在，我们有了三个超现实数 \(-1,0,1\) ，它们可以组合成 \(8\) 个集合： \[ \{\},\{-1\},\{0\},\{1\},\{-1,0\},\{-1,1\},\{0,1\},\{-1,0,1\} \] 我们可以用这些集合作为 \(L\) 和 \(R\) 继续构造超现实数，但符合定义的只有： \[ \{|R\},\{L|\},\{-1|0\},\{-1|0,1\},\{-1|1\},\{0|1\},\{-1,0|1\} \] 可以证明，\(\{1|\}>1\) ，因此我们令 \(\{1|\}=2\) ，而 \(0<\{0|1\}<1\) ，令 \(\{0|1\}=\frac{1}{2}\) ，同理有 \(\{|-1\}=-2,\{-1|0\}=-\frac{1}{2}\) 。而 \(\{0,1|\}\) 又是多少呢？可以发现 \(\{0,1|\}\ge \{1|\}\) 且 \(\{0,1|\}\le \{1|\}\) ，所以有 \(\{0,1|\}=\{1|\}=2\) 。同理，可以得到： \[ \begin{aligned} -2&=\{|-1\}=\{|-1,0\}=\{|-1,1\}=\{|-1,0,1\}\\ -1&=\{|0\}=\{|0,1\}\\ -\tfrac{1}{2}&=\{-1|0\}=\{-1|0,1\}\\ 0&=\{|\}=\{-1|\}=\{|1\}=\{-1|1\}\\ \tfrac{1}{2}&=\{0|1\}=\{-1,0|1\}\\ 1&=\{0|\}=\{-1,0|\}\\ 2&=\{1|\}=\{0,1|\}=\{-1,1|\}=\{-1,0,1|\} \end{aligned} \]

而根据这些新的超现实数，我们又可以得到更多的超现实数，如果称 \(0\) 是第一天“出生”的数，\(-1\) 和 \(1\) 是第二天出生的数，上面几个数是第三天出生的数，那么假设 \(x^L\) 和 \(x^R\) 最大的出生日期是 \(k\) ，我们称 \(x\) 为第 \(k+1\) 出生的。

不过，让我们暂且停下来，讨论点别的，毕竟这种“代表”只是我们的一种假设，它是否合理还有待验证。

一些定理

定理 0：对于一个超现实数 \(x\) ，有：

  1. \(x\ngeq x^R\) ,
  2. \(x^L\ngeq x\) ,
  3. \(x\ge x\) ,
  4. \(x=x\) .

似乎证明这个很简单：

  1. 令 \(y=x^R\) ，那么有 \(x^R\leq y\) ，这里假设我们证明了 \(x^R\le x^R\) ，那么有 \(x\ngeq y\) 。
  2. 同理。
  3. 令 \(y=x\) ，那么 \(x^R\nleq y\) 且 \(x\nleq y^L\) 。
  4. 因为 \(x\ge x\) 且 \(x\le x\) ，所以 \(x=x\) 。

看起来一切很美妙，但我们发现一个奇怪的事：要证明 \(x\ngeq x^R\) 和 \(x^L \ngeq x\) 就必须证明 \(x^R\ge x^R\) 和 $xLxL $ ，而证明 \(x^R\ge x^R\) 即证明 \(x\ge x\) ，又需要前面两个结论——发生了循环论证。

由于超现实数递归的本质，我们要证明关于它的结论，最好的办法就是数学归纳法。注意到，对于简单的情况，例如 \(x=\{\varnothing|\varnothing\}=0\) ——所有超现实数的起源，这是成立的。因此，假设比 \(x\) 更早出生的数 \(x^L\) 和 \(x^R\) 都满足上述定理，那么根据上述证明显然 \(x\) 也满足。

定理 1：若 \(x\ge y\) 且 \(y\ge z\) ，那么有 \(x\ge z\) 。（即 \(\ge\) 关系的传递性）

证明：同样使用数学归纳法。设 \(\alpha=\{|\}\) ，令 \(\beta=\{\alpha|\},\gamma=\{|\alpha\}\) ，那么有 \(\beta\ge \alpha\) 和 \(\alpha\ge \gamma\) ，同时我们也能证明 \(\beta\ge \gamma\) ，显然这三个数任意组合都是满足这个定理的。

设 \(x,y,z\) 的出生日期之和为 \(n\) ，且我们已经证明了出生日期之和小于 \(n\) 的三元组都满足这个定理，那么若 \(x\ngeq z\) ，则有 \(x^R\le z\) 或 \(x\le z^L\) 成立：

  • 若 \(x^R\le z\) ，且 \(z\le y\) ， \(y,z,x^R\) 的出生日期之和小于 \(n\) ，那么 \(x^R\le y\) ，所以 \(x\ngeq y\) ，矛盾。
  • 若 \(x\le z^L\) ，且 \(y\le x\) ， \(z^L,x,y\) 的出生日期之和小于 \(n\) ，那么 \(y\le z^L\) ，所以 \(y\ngeq z\) ，矛盾。

故 \(x^R\nleq z\) 且 \(x\nleq z^L\) ，所以 \(x\ge z\) 。

定理 2：若 \(x\ngeq y\) ，则 \(x\le y\) 。

这看上去很显然，但我们前面说过，这是一套新的数学系统，因此我们需要严谨的证明它。

在此之前，我们先证明 \(x^L\le x\le x^R\) 。要证明 \(x\ge x^L\) ，即证明 \(x^R\nleq x^L\) 且 \(x\nleq (x^L)^L\) ，前者显然是成立的（根据定义）， 而后者，根据归纳假设，有 \(x^L\ge (x^L)^L\) ，那么若存在 \(x\le (x^L)^L\) ，则有 \(x^L\ge x\) ，与定理 0 矛盾，因此 \(x^L\le x\) 成立，同理可得 \(x\le x^R\) 成立。更进一步，有 \(x^L\lt x\lt x^R\) 。

若 \(x\ngeq y\) ，那么存在 \(x^R\le y\) 或者 \(x\le y^L\) ，对于前者，由于 \(x\le x^R\) ，那么根据传递性有 \(x\le y\) ，对于后者，由于 \(y^L\le y\) ，根据传递性也有 \(x\le y\) 。进一步的，有 \(x\lt y\) ，此时超现实数的定义我们就可以说成”左集合的所有数都小于右集合“了， \(\ngeq\) 也可以直接用 \(\lt\) 来代替了。

但是，“若 \(x\ge y\) 则 \(x\nleq y\) ”是错的，\(x\ge y\) 和 \(x\le y\) 可能同时成立，根据之前的定义我们称之为 \(x=y\) ，但这并不就意味着 \(x\) 和 \(y\) 是完全相同的（例如 \(\{|0\}=\{|0,1\}\)），应该称之为相似，或者说，它们属于等价类。不过为了简便，我们都称之为相等。

所以，超现实数集满足反对称性、传递性和完全性，有全序关系。进一步的，它还满足严格全序关系。

关于加法和 \(-x\)

在上面我们定义了超现实数的加法：

\(x+y=\{x^L+y,x+y^L|x^R+y,x+y^R\}\) 。

但两个数相加产生的数是否还满足超现实数的定义呢？我们需要证明这一点。

首先来试试这种加法运算，还是设 \(\alpha=\{|\}\) ，令 \(\beta=\{\alpha|\},\gamma=\{|\alpha\}\) ，发现 \(\alpha+\alpha=\{|\}=\alpha\) ，\(\alpha+\beta=\{\alpha+\alpha|\}=\beta\) ，\(\alpha+\gamma=\{|\alpha+\alpha\}=\gamma\) 。看上去对于简单的情况都是 ok 的。

那么对于复杂的情况呢？我们还没法证明加法的结果就是数因为可能存在左集合数大于等于右集合数的情况，让我们称这种数为伪数。

定理 0：\(\alpha+x=x\) 。

我们已经证明了 \(\alpha+\alpha\) 以及 \(\alpha+\beta,\alpha+\gamma\) 的情况，假设对于 \(x^L\) 和 \(x^R\) 都成立，那么 \(\alpha+x=\{\alpha+x^L|\alpha+x^R\}=\{x^L|x^R\}=x\) 。

同理，我们还能证明 \(x+\alpha=x\) ，所以 \(\alpha\) 其实就是超现实数在加法操作中的零元！这个时候，我们有理由说令 \(\{|\}=0\) 是合理的了。

此定理对于伪数同样成立。

定理 1：\(x+y=y+x\) ，即交换律

可以先对 \(\beta+\gamma=\gamma+\beta\) 进行验证，发现是满足的。

假设 \(x^L,x^R,y^L,y^R\) 都是满足的，那么：

\[ \begin{aligned} x+y&=\{x^L+y,x+y^L|x^R+y,x+y^R\}​\\ y+x&=\{y+x^L,y^L+x|y+x^R,y^R+x\} \end{aligned} \]

根据归纳假设，其左集合和右集合元素完全相同，因此 \(x+y=y+x\) 。

此定理对于伪数也同样成立。

定理 2：\((x+y)+z=x+(y+z)\) ，即结合律

\[ \begin{aligned} (x+y)+z&=\{x^L+y,x+y^L|x^R+y,x+y^R\}+z\\ &=\{x^L+y+z,x+y^L+z,x+y+z^L|x^R+y+z,x+y^R+z,x+y+z^R\} \end{aligned} \]

而 \(x+(y+z)\) 结果的表达式不再写出，相信你根据上式已经了解，同样使用归纳法可以证明其相等。

此定理对于伪数也同样成立。

定理 3：若 \(x\ge y\) 且 \(p\ge q\) ，那么 \(x+p\ge y+q\) 。

引理：若 \(x+p\ge y+q\) 且 \(p\le q\) ，那么 \(x\ge y\) 。

我们可以同时对定理和引理进行归纳证明。

证明此定理即证明 \(x^R+p\nleq y+q\) ，\(x+p^R\nleq y+q\) ，\(x+p\nleq y^L+q\) ，\(x+p\nleq y+q^L\) 。

对于 \(x^R+p\nleq y+q\) ，假设存在 \(y+q\ge x^R+p\) ，因为 \(q\le p\) ，根据引理的归纳假设，有 \(y\ge x^R\) ，又 \(x\ge y\) ，根据传递性 \(x\ge x^R\) ，而我们已经证明了这是不可能的。对于另外三个同理可证。

而对于引理，若 \(x\ge y\) 不成立，那么 \(x^R\le y\) 或者 \(x\le y^L\) 中至少有一种情况会出现，对于前者，因为 \(x^R\gt x\ge y\) ，矛盾，对于后者，因为 \(x\ge y\gt y^L\) ，矛盾。

同时，我们还可以证明：若 \(x\ge y\) 且 \(p\gt q\) ，那么 \(x+p\gt y+q\) 。首先 \(x+p\ge y+q\) 是肯定的，要证明的是 \(x+p\nleq y+q\) ，由于 \(x\ge y\) ，若 \(x+p\leq y+q\) ，那么必然有 \(p\leq q\) ，这与假设矛盾。

现在，再让我们回过头来看看加法的定义，同样使用归纳法，假设 \(x^L+y,x+y^L,x^R+y,x+y^R\)​​ 都是数，那么我们只需要证明 \(x^L+y,x+y^L\)​​ 都小于 \(x^R+y,x+y^R\)​​​​​​ ，这时候只要我们用归纳法同时证明定理 3 和加法即可，这里不再赘述。到此，我们证明了加法的结果也是一个符合定义的超现实数。

定理 4：\(x+(-x)=\alpha\) ，即 \(-x\) 为加法逆元。

回顾一下，\(-x=\{-x^R|-x^L\}\) ，那么有 \(-\alpha=\alpha\) ，我们还发现 \(-\beta=\gamma\) ，而 \(\beta+\gamma=\{\alpha+\gamma|\beta+\alpha\}=\{\gamma|\beta\}\) ，而 \(\{\gamma|\beta\}\ge a\) 且 \(a\ge\{\gamma|\beta\}\) ，因此 \(\beta+\gamma=\alpha\) 。

对于一般的情况，\(x+(-x)=\{x^L+(-x),x+(-x^R)|x^R+(-x),x+(-x^L)\}\) ，我们先证明它是大于等于 \(\alpha\) 的，即证明 \(x^R+(-x)\gt\alpha\) 且 \(x+(-x^L)\gt\alpha\) ，对于前者， 由于 \(-x\gt -x^R\) ，\(x^R+(-x)\gt x^R+(-x^R)\) ，而根据归纳假设，后者等于 \(\alpha\) ，对于 \(x+(-x^L)\gt \alpha\) 的证明同理，故 \(x+(-x)\ge \alpha\) ，同理可证 \(x+(-x)\le \alpha\) ，故 \(x+(-x)=\alpha\) 。此时我们也可以定义减法了：\(x-y\) 即 \(x+(-y)\) 。

定理 5：\(-(x+y)=(-x)+(-y)\) 。

定理 6：若 \(x\le y\) ，则 \(-y\le -x\) 。

证明方法都与上面类似，不再赘述。

综上，在加法定义下，超现实数是一个阿贝尔群。

关于乘法和逆元

还记得乘法的定义吗：

\(xy=\{x^Ly+xy^L-x^Ly^L,x^Ry+xy^R-x^Ry^R|x^Ly+xy^R-x^Ly^R,x^Ry+xy^L-x^Ry^L\}\)

同样，在我们证明它是个超现实数之前，先假定它就是个数。

定理 0：\(xy=yx\) ，即乘法的交换律。

归纳即可。

此定理对于伪数也同样成立。

定理 1：\(0y=0\) ，即零元。

显然结果的左右集合都是空，再次印证了 \(\alpha\) 为 \(0\) 的合理性。

此定理对于伪数也同样成立。

定理 2：\(1y=y\) ，即单位元。

\(1y=\{0y+1y^L-0y^L|0y+1y^R-0y^R\}=\{y^L|y^R\}=y\) ，这里同样用到了归纳法。印证了 \(\beta\) 作为 \(1\) 的合理性。

此定理对于伪数也同样成立。

定理 3：\(-(xy)=(-x)y\) 。

\[ \begin{aligned} (-x)y=\{-x^R|-x^L\}\times y =&\{(-x^R)y+(-x)y^L-(-x^R)y^L,(-x^L)y+(-x)y^R-(-x^R)y^R| \\ &(-x^R)y+(-x)y^R-(-x^R)y^R,(-x^L)y+(-x)y^L-(-x^L)y^L\} \end{aligned} \]

通过归纳法，可以得证。

此定理对于伪数也同样成立。

定理 4：\(x(y+z)=xy+xz\) ，即对加法的分配律。

定理 5：\(x(yz)=(xy)z\) ，即乘法的结合律。

证明方法也没什么特别的。

此两条定理对于伪数也同样成立。

定理 6：若 \(x\gt x'\) 且 \(y\gt y'\) ，那么 \((x-x')(y-y')\gt 0\) 。

首先要提出一点，无论乘法的结果是不是个数，定理 4 都是成立的。

把乘法的定义和定理 6 一起来看：

我们要证明乘法结果是数，那么就要证明其左集合的数小于右集合的数，例如：\(x^Ly+xy^L-x^Ly^L\lt x^Ly+xy^R-x^Ly^R\) ，化简后得到：\((x-x^L)(y^R-y^L)\gt 0\) 。

另外三个式子为：\((x^R-x)(y^R-y^L)\gt 0,(x^R-x^L)(y-y^L)\gt 0,(x^R-x^L)(y^R-y)\gt 0\) 。

那么我们需要 \(xy^R,xy^L,x^Ry,x^Ly,x^Ly^R,x^Ly^L,x^Ry^R,x^Ry^L\) 都是数，好在这可以通过归纳法来假设。

那么，\((x-x^L)(y^R-y^L)\) 等也必然是个数，

用有理数来表示超现实数

我们知道，用 \(0\) 来表示 \(\alpha\) 是合理的，因为它就是零元。至于用 \(1,-1\) 来表示 \(\beta,\gamma\) 的合理性，需要在我们讨论乘法时再说明。事实上，仅考虑加法的情况下，用什么数来表示 \(\beta,\gamma\) 实际上无所谓，无非就是 \(1\) 代表了一个单位而已，毕竟这里所谓的“合理”，指的是大小关系和运算结果都能对的上。

定理 0：若 \(y^L\lt x\lt y^R\) ，那么 \(x=\{x^L,y^L|x^R,y^R\}\) 。

令等式右边的数为 \(z\) ，显然它满足“数”的定义，并且 \(x\ge z\) 且 \(x\le z\) 都很容易证明。

同时，我们可以发现，若 \(x_{max}^L\) 是 \(x^L\) 中“最大”的那个数（因为是全序的），\(x_{min}^R\) 为 \(x^R\) 中最小的那个数，那么 \(x=\{x_{max}^L|x_{min}^R\}\) 。利用此定理即可证。

那么，假设我们在前 \(n\) 天创造出了 \(m\) 个数 \(x_1\lt x_2\lt \dots\lt x_m\) ，那么，在第 \(n+1\) 天，只会新创造出 \(m+1\) 个数： \[ \begin{aligned} \{&|x_1\}\\ \{x_1&|x_2\}\\ \dots\\ \{x_{m-1}&|x_m\}\\ \{x_m&|\} \end{aligned} \] 要如何证明这个结论呢？首先，对于 \(\{x_{i-1}|x_{i+1}\}\) ，根据定理 0，有 \(x_i=\{x_{i-1},x_i^L|x_{i+1},x_i^R\}\) 且 \(\{x_{i-1}|x_{i+1}\}=\{x_{i-1},x_i^L|x_{i+1},x_i^R\}\) ，根据传递性 \(x_i=\{x_{i-1}|x_{i+1}\}\) 。

而对于 \(\{x_{i-1}|x_{j+1}\},i\lt j\) 这样的数呢？它等于 \(x_i\) 到 \(x_j\) 中最早出生的数。无论如何，我们都可以通过定理 0 来证明这个。若有多个最早出生的数，这说明这几个数相等，这是不可能的。此时我们可以得到下面这个定理。

定理 1：若 \(x=\{x^L|x^R\}\) ，且 \(y\) 是满足 \(x^L\lt y\lt x^R\) 的数中最早出生的数，那么 \(x=y\) 。

故，在前 \(n\) 天总共出生了 \(2^n-1\) 个数。

回到前面的问题，我们如何用有理数表示第 3 天之后出生的数呢？

在前 2 天，我们得到了 \(-1,0,1\) 三个数，那么第 3 天会得到 4 个新的数 \(\{|-1\},\{-1|0\},\{0|1\},\{1|\}\) ，我们发现，\(1+1=\{0+1|\}=\{1|\}\) ，因此 \(\{1|\}=2\) ，同理 \(\{|-1\}=-2\) 。

那么，假设我们已经证明了第 \(k\) 天生成的最大的数 \(x\) 以及第 \(k+1\) 生成最大的数 \(y=\{x|\}\) 满足 \(y=x+1\) ，那么对于第 \(k+2\) 天生成的最大的数 \(\{y|\}\) ，有 \(y+1=\{y,x+1|\}=\{y|\}\) 。

因此，令第 \(n+1\) 天生成的最大的数是有理数 \(n\) 是合理的，最小的数为 \(-n\) 同理。

那么对于 \(\{x_i|x_{i+1}\}\) 呢？先看看 \(\{0|1\}\) ，令 \(b=\{0|1\}\) 则有 \(b+b=\{b|b+1\}\) ，根据定理 1，我们可以发现 \(b+b=1\) ，因此 \(b=\frac{1}{2}\) 是合理的。一般的，​ \[ \begin{aligned} \{x_i|x_{i+1}\}+\{x_i|x_{i+1}\}&=\{x_i^L+x_{i+1},x_i+x_{i+1}^L|x_i^R+x_{i+1},x_i+x_{i+1}^R\}\\ &=x_i+x_{i+1} \end{aligned} \] 那么，有 \(\{x_i|x_{i+1}\}=\frac{x_i+x_{i+1}}{2}\) 。

回到游戏

可以发现，一个超现实数和一个 Blue-Red Hackenbush 的图是一致的：构造方法是一致的，比较符号以及 \(x+y\) 和 \(-x\)​​ 的定义也都是一致的。因此，每个局面都可以用一个有理数来表示。

那么如何计算一个局面的值呢？

链

先考虑只有一种颜色的链，根据定义很显然边长为 \(x\) 的蓝链值为 \(x\) ，边长为 \(x\) 的红链值为 \(-x\)​​ 。

实际上，一条链的值和上面超现实数的生成方法是等价的，长为 \(n\) 的值为第 \(n+1\)​ 天生成的某个数，参考下图一目了然：

树

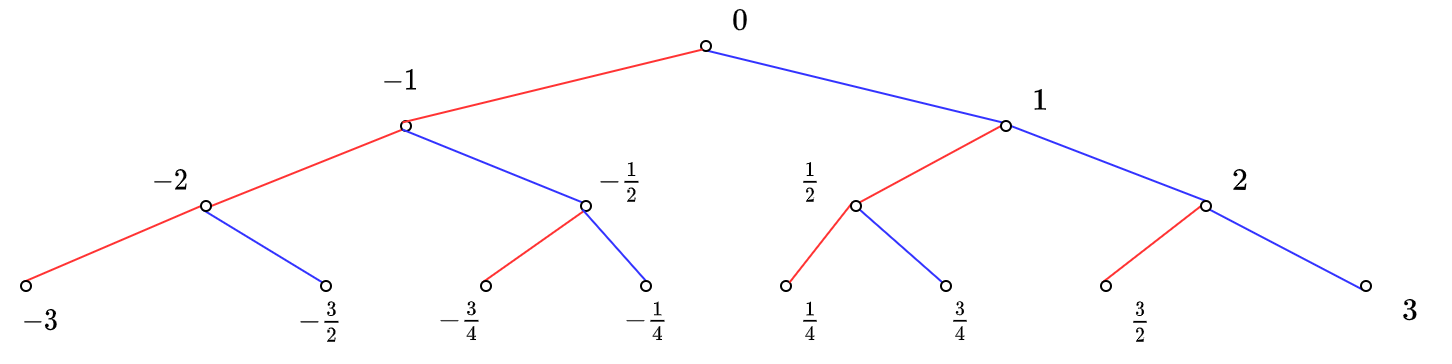
根到点的路径构成了一条链，而其祖先的任意点，都是游戏下一步能到达的状态。

计算一条链（即树的某个点）的具体值的方法也很容易，就不做说明了。

树

和 Green Hackenbush 的方法是类似的，遇到分岔时，以一条链代替所有子树的游戏和，这里不再给出证明，例如：

树

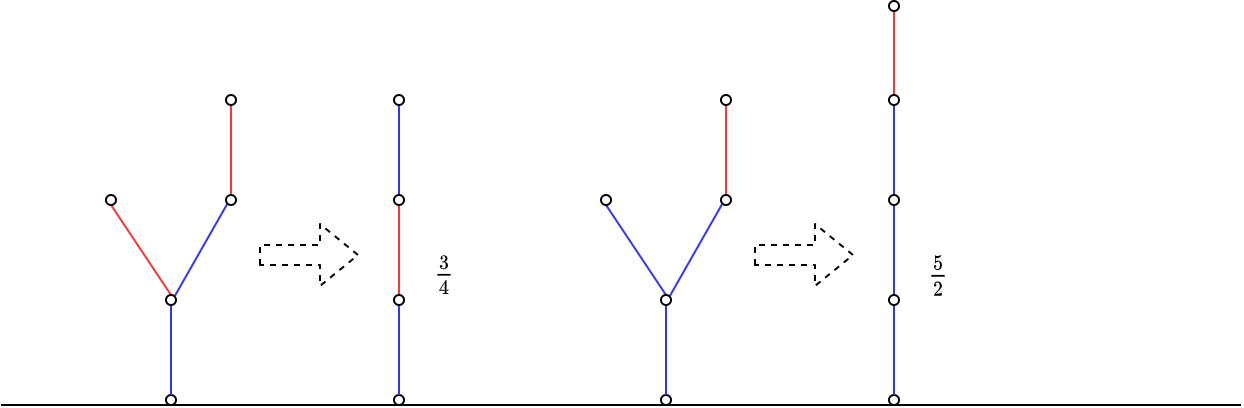
图

Blue-Red-Green Hackenbush

待更

参考资料